Tu sei qui
demistifichiamo l'emagramma, il "temp" ed il riscaldamento dell'atmosfera
Demistifichiamo l'emagramma, il ''temp'' ed il riscaldamento dell'atmosfera
- Contents
- Demistifichiamo l'emagramma, il ''temp'' e il riscaldamento dell'atmosfera, I parte
- Demistifichiamo l'emagramma, il "temp" e il riscaldamento dell'atmosfera, II parte
- Demistifichiamo l'emagramma, il "temp" e il riscaldamento dell'atmosfera, III parte
- Demistifichiamo l'emagramma, il "temp" e il riscaldamento dell'atmosfera, IV parte
- Demistifichiamo l'emagramma, il "temp" e il riscaldamento dell'atmosfera, V parte
- Demistifichiamo l'emagramma, il "temp" e il riscaldamento dell'atmosfera, VI parte
- Demistifichiamo l'emagramma, il "temp" e il riscaldamento dell'atmosfera, VII parte
- About this document ...
- versione non impaginata (su un'unica pagina)
|
questo testo può essere diffuso liberamente a patto che ciò sia fatto senza fini di lucro, non sia apportata alcuna modifica a forma e contenuto e siano citati i nomi di autore (Jean Oberson) e traduttore (Tiberio Galletti) nonché le fonti dell'articolo originale (www.soaringmeteo.com) e della versione tradotta (sulparapendio.altervista.org, |
Tiberio G. 2006-12-27
I parte
Dopo il mio articolo sui modelli numerici apparso sul numero di aprile di ``Swiss Glider'' che trattava, tra l'altro, dei sondaggi virtuali (calcolati e previsti), quindi di ``temp'' e di emagrammi, diversi piloti mi hanno chiesto come funzionasse l'interpretazione di tali grafici. Ciò è di fondamentale importanza se si vuole interpretare in maniera valida le condizioni atmosferiche ai fini del volo, specialmente se di distanza. Dà, in effetti, quasi tutte le informazioni necessarie e si potrà quasi ignorare le altre informazioni meteo. Nel 1985, Heinrich Rotach, pubblicò in "Delta info", antenato di "Swiss Glider", un articolo molto ben fatto che mi ha rivelato l'analisi e l'interpretazione di questi grafici. Da quel momento, ho potuto sperimentare ed affinare la comprensione di tutte quelle nozioni confrontando le condizioni di volo, che ho vissuto personalmente o che altri piloti hanno riportato, con lo stato dell'atmosfera perfettamente riassunto nel "temp". In questa serie di articoli è mia intenzione parlarvene nel modo più semplice possibile.
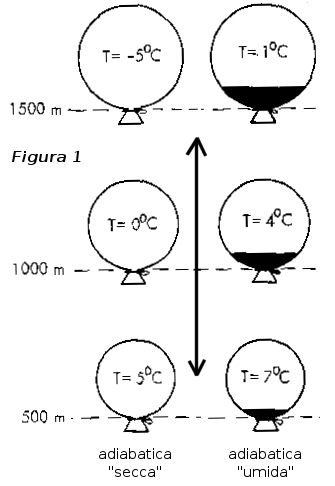
L'emagramma è un semplice grafico XY, come tutti abbiamo incontrato a scuola. In X si hanno le temperature dell'aria ed in Y l'altitudine. Niente di complicato (ved. figura 1). La difficoltà viene dal fatto che i meteorologi, per facilitare i loro calcoli, utilizzano le pressioni atmosferiche per rappresentare l'altitudine nell'asse Y. Attualmente la pressione atmosferica si misura in hectopascal (hPa); fortunatamente un 1 hPa è uguale a 1 mbar. Tenete in mente che la pressione atmosferica diminuisce di un valore preciso con l'aumento dell'altitudine. E' dunque comprensibile, anche se per noi innaturale, rappresentare l'altitudine attraverso dei valori di pressione atmosferica. Si sono scelti dei valori standard di pressione, chiamati geopotenziali: per esempio geopotenziali 850, 700 e 500 sono utilizzati molto spesso. Si può immaginare il geopotenziale come una superficie virtuale orizzontale ad una certa altitudine nell'atmosfera, intorno alla terra, i cui punti hanno tutti una pressione identica. In più, per complicare le cose, la pressione atmosferica in un punto evolve nel tempo in maniera irregolare e complessa a seconda delle condizioni meteo. Il geopotenziale non è dunque una superficie piana bensì leggermente ondulata. In inverno ed in caso di maltempo, i geopotenziali 850hPa, 700hPa e 500hPa stazionano al disotto, rispettivamente, di 1500m, 3050m e 5500m. In estate ed in caso di bel tempo si trovano, invece, al disopra di questi valori.
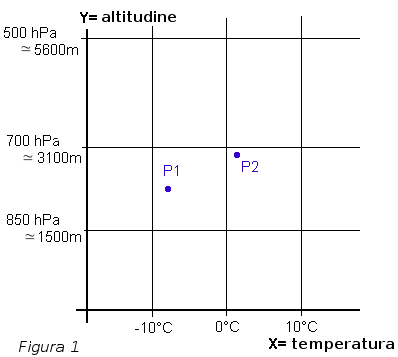
Sul grafico precedente (fig. 1), abbiamo il nostro primo emagramma semplificato. Penso che nessuno abbia difficoltà a comprenderlo. Le temperature sono rappresentate in gradi Celsius (°C). Questa rappresentazione è più classica e più facile da capire di quella delle pressioni per l'altitudine. L'isoterma (da non confondere con isotermia) è una retta perpendicolare (qui verticale) che parte da una temperatura scelta sull'asse X e che rappresenta l'insieme dei punti del grafico a questa stessa temperatura. Nei bollettini meteorologici, si parla spesso dell'altitudine dell'isoterma dello zero °C. Si vuol dire semplicemente a quale altitudine si incontrerà questa temperatura di riferimento. Il punto P1 per esempio di trova sull'isoterma -8°C all'altitudine di 2300m circa. Il punto P2 si trova sull'isoterma +1,5°C verso 3000m.
Andiamo avanti. Un'altra difficoltà che può subentrare alla lettura del vero emagramma viene dal fatto che l'asse X delle temperature non è perpendicolare all'asse Y, come sul grafico precedente. Precisazione: per noi vololiberisti, non necessariamente fisici, può bastare nonostante tutto rimanere ai due assi XY perpendicolari visto che può risultare più facile da comprendere. I ragionamenti e l'utilizzo del pilota restano precisamente identici. Continuiamo comunque un po' con il vero emagramma per prenderci familiarità. Guardate il grafico qua sotto (fig. 2). Si tratta dello stesso grafico XY di cui sopra, con i due esempio P1 e P2, nello stesso punto (alle stesse coordinate), ma l'asse X è inclinato verso il basso e, conseguentemente, le isoterme, perpendicolari ad X, sono inclinate da sinistra a destra.
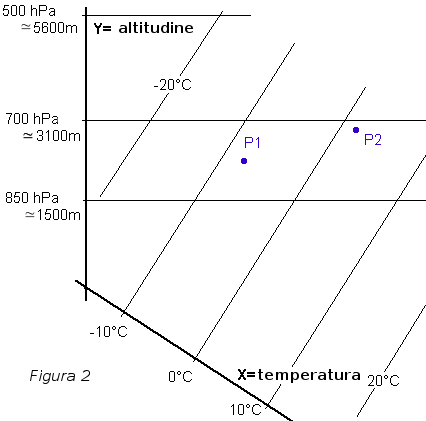
Nella pratica non si rappresenta l'asse X ma solamente le isoterme: guardate il grafico successivo (fig. 3).
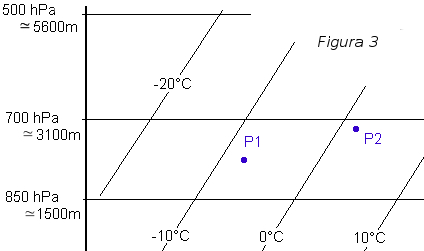
Guardate ora un vero emagramma (fig. 4) ignorando per adesso tutte le altre curve non ancora affrontate, dovreste ritrovare l'asse Y dell'altitudine, con le sue pressioni atmosferiche, e le isoterme inclinate.
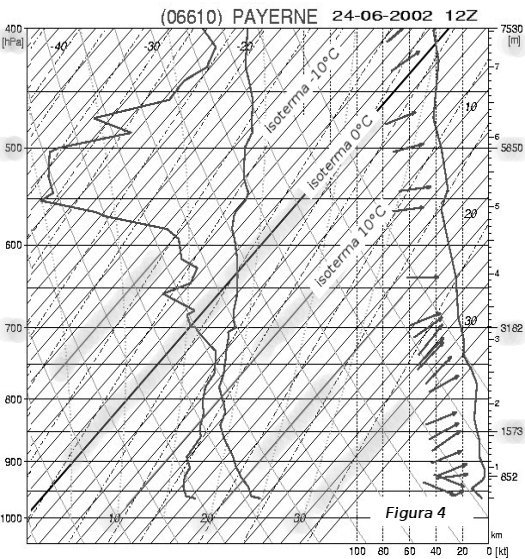
Il "temp" è il risultato grafico delle misure del radiosondaggio. Questo risultato è riportato (disegnato) sull'emagramma (v. fig. 5) ed esprime, alle differenti altitudini:
- i valori (curva) della temperatura dell'aria in °C;
- i valori (curva) d'umidità dell'aria espressi in temperatura del punto di rugiada;
- i valori (curva o numeri) della velocità del vento e
- la direzione del vento (di solito delle piccole frecce)
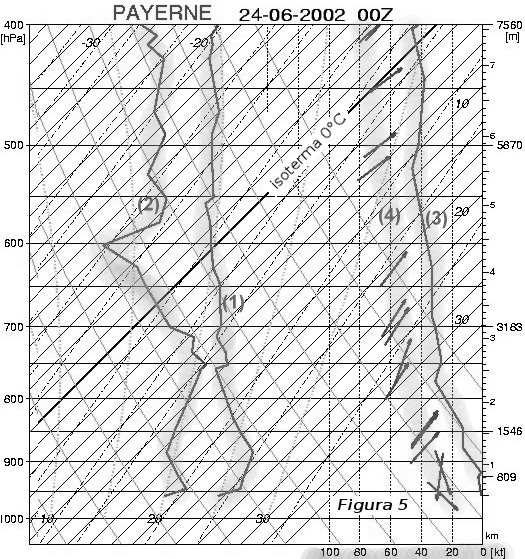
Qualche osservazione sulla figura 5: i dati inerenti il vento si trovano dunque a destra del grafico. La direzione alle varie altitudini è indicata da delle piccole frecce. Per esempio, una freccia che punta a destra indica un vento proveniente da Ovest. La velocità alle varie altitudini ha la forma di una curva (curva 4) dove i valori espressi in nodi (kt) si proiettano sull'asse X, in basso a destra. Ricordiamo che 1kt corrisponde a 1,85km/h. I valori della velocità aumentano da destra a sinistra contrariamente ai valori della temperatura, sullo stesso asse, che aumentano obliquamente da sinistra a destra. L'isoterma dello zero °C incrocia la curva della temperatura (1) verso 4300m circa. Potete notare che le altezze dei geopotenziali non sono identiche tra le figure 4 e 5, nonostante sia lo stesso giorno e cambi solo l'ora: la figura 5 mostra il "temp" a mezzanotte mentre la figura 4 mostra il "temp" di mezzogiorno. Per esempio, il geopotenziale 500hPa sopra Payerne è all'altitudine di 5870m a mezzanotte e a 5850m a mezzogiorno.
Nota: una radiosonda è un dispositivo composto da un pallone ascensionale ed un apparecchio di misurazione dell'aria (temperatura, umidità e venti) che è lasciato nella troposfera (a circa 10000m d'altitudine) due volte al giorno dagli istituti meteorologici di ogni paese. Per permettere un utilizzo razionale da parte di tutti, questi radiosondaggi sono effettuati nello stesso momento a mezzogiorno UTC (ora universale) ovvero 12Z e a mezzanotte UTC ovvero 00Z. L'ora universale è quella di Greenwich. In estate, 12Z=14h00 da noi; in inverno, 12Z=13h00. In Svizzera non c'è che un solo posto dove ha luogo regolarmente il radiosondaggio: Peyerne. In Europa se ne possono inoltre trovare molti altri tra cui quelli di Monaco, di Lione e di Milano, per esempio.
Abbiamo comunque un problema: il "temp", per preciso che sia, può presentare dei piccoli errori di misurazione ma soprattutto può cambiare in maniera significativa in qualche ora seguendo l'evoluzione meteo. I valori di mezzanotte possono dunque non obbligatoriamente corrispondere a quelli del pomeriggio seguente, durante il quale andremo a volare. Oltretutto la topografia può fortemente influenzare il "temp" locale differenziandolo da quello di Payerne. Penso in particolare alle coste lacustri e alle valli montane. Ciò significa che si possono trovare delle condizioni di volo forti in una regione e calma piatta in un'altra, anche se non molto lontana, nello stesso giorno.
II parte
Nella prima parte, abbiamo visto che l'emagramma era un semplice grafico XY con, in Y, l'altitudine in unità di pressione atmosferica e, in X, la temperatura in cui l'asse è nascosto e le isoterme sono inclinate. Abbiamo anche visto che su questo grafico si può disegnare il risultato d'un radiosondaggio sotto forma di curva chiamata "temp".
Prima di andare avanti, confrontiamo l'andatura dello stesso "temp" in due emagrammi con disposizione differente: il primo ortogonale (fig. 1) ed il secondo classico (fig. 2). A sinistra si vede la curva d'umidità e a destra quella delle temperature.
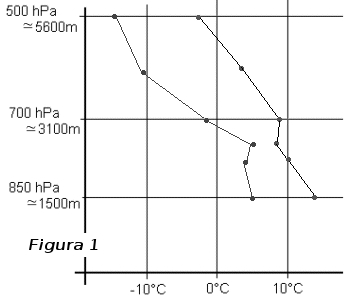
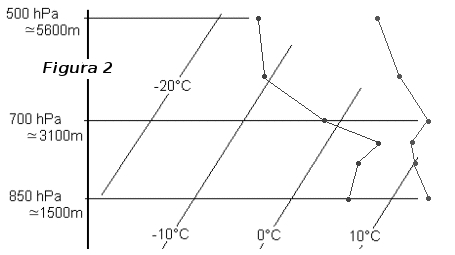
Con i venti (qui non rappresentati) il "temp" mostra dunque "le curve di stato": curve di temperatura, d'umidità e dei venti che descrivono, attraverso i loro valori, l'atmosfera in un preciso momento e luogo. Attenzione a non fare confusione con le curve dette "adiabatiche" che descrivono l'evoluzione d'una massa d'aria in movimento verticale; queste saranno trattate più avanti.
Ancora una volta le curve della figura 1 sono strettamente identiche a quelle della figura 2 (verificate, prego). A causa delle isoterme inclinate nella figura 2, le forme delle curve sono differenti tra le due figure. E' vero che la disposizione delle curve della figura 1 ci sembra più esplicita e che la loro interpretazione è più immediata rispetto a quella delle curve in figura 2, ma può essere utile capire bene la differenza e non sentirsi spiazzati di fronte ad un emagramma non ortogonale.
Esaminiamo intanto da più vicino le curve della temperatura. Per prima la curva delle ore 00h00UTC, 02h00CEST (Central European Summer Time: ora estiva per l'Europa centrale; altrimenti conosciuta, da noi, come "ora legale"). Ciascuna notte presenta una curva differente ma si può descrivere l'andamento generale d'una curva di una notte chiara (senza nuvole) e senza venti significativi di fine primavera o inizio estate (fig. 3).
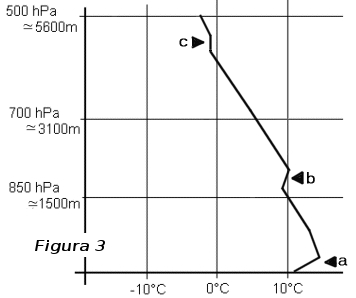
Una breve rinfrescata: normalmente la temperatura decresce con l'altitudine. Esistono comunque delle fasce dove la temperatura cresce, dette fasce d'inversione di temperatura, o semplicemente d'inversione, e delle fasce dove la temperatura resta identica, dette fasce d'isotermia (da non confondere con isoterma). Durante le notti chiare e senza vento (in poche parole le notti che precedono spesso le giornate di buone condizioni di volo), il suolo perde rapidamente il calore e raffredda sensibilmente anche la bassa atmosfera. Ciò fa si che l'aria sia più fredda vicino al suolo che a qualche decina di metri più in alto. Si forma, dunque, un'inversione di temperatura al suolo (fig. 3, a), molto marcata, di circa 5°C su circa 200-300m. E' ciò che accade sempre in una notte serena e senza vento. Questo fenomeno è invece ostacolato da una forte nuvolosità (blocco della perdita di calore) e/o da forte vento al suolo (rimescolio dell'aria). Più in alto la temperatura diminuisce in maniera più o meno regolare. Talvolta (non sempre) si possono incontrare delle isotermie (fig. 3, c) e delle inversioni (fig. 3, b) più o meno marcate, in altitudine. La diminuzione media della temperatura è espressa dal gradiente medio di temperatura in °C ogni 100m. Per esempio: se si hanno -2°C a 4000m e 10°C a 2000m inversioni e isotermie comprese, il gradiente medio di temperatura sarà di 12°C in 2000m quindi 0.6°C ogni 100m. In generale il gradiente medio di temperatura in altitudine (sopra la fascia di inversione al suolo) varia tra 0,3°C/100m e 0,85°C/100m secondo le condizioni meteo ed il tipo di massa d'aria. In quasi 10 anni d'osservazione assidua, non ho mai riscontrato gradienti superiori a 0,9°C/100m.
Nel bel mezzo di una giornata assolata (non parlerò, evidentemente, delle giornate coperte), le cose cambiano (fig. 4).
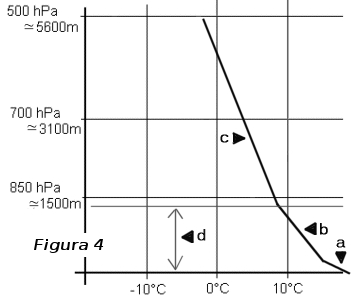
Il suolo, surriscaldato dal sole, ridistribuisce questo calore alla bassa atmosfera adiacente. Ci si può quindi aspettare un calo più marcato della temperatura. In a (fig. 4), il gradiente termico supera 1°C/100m per qualche decina di metri sopra il suolo. Più in alto, in b, si incontra una fascia di qualche centinaio di metri dove il gradiente di temperatura è uguale a 1°C/100m. In a si dice che il gradiente è sovradiabatico ed in b che è adiabatico (più avanti ne vedremo i motivi). Ad un'altitudine maggiore, in c, si incontra un gradiente variante tra 0,3°C/100m e 0,85°C/100m secondo le condizioni meteo e il tipo di massa d'aria. Si possono nuovamente incontrare fasce d'inversione o d'isotermia, ma non obbligatoriamente. La fascia in a ed in b, adiacente al suolo, è chiamata fascia convettiva (fig. 4, d). E' a questo livello e solamente a questo che hanno luogo i fenomeni convettivi (quindi le ascendenze termiche, che noi adoriamo, e le discendenze a loro associate, che disprezziamo). Per gli impazienti, ma vedremo i dettagli più avanti, anticipiamo che più la fascia convettiva è spessa, più alti saranno i plafond e più forti le termiche. In c, non ci sono, in teoria, movimenti verticali convettivi. Intuitivamente, si può comunque già dedurre che più il gradiente di temperatura in c, appena sopra alla fascia convettiva, è grande e più che la fascia convettiva sottostante sarà spessa, e dunque migliori saranno le ascendenze convettive.
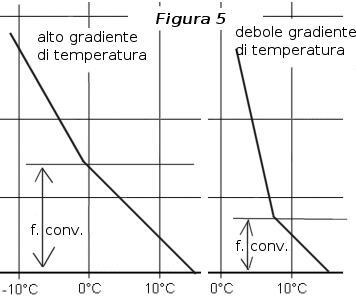
Si comprende quindi l'importanza del gradiente di temperatura nelle fasce di media altitudine sulla qualità delle ascendenze termiche (fig. 5). Si tratta di un esempio costruito. A sinistra il gradiente (=gdt) di temperatura alle medie altitudini è forte (per esempio 0,8°C/100m) il che comporta una fascia convettiva spessa, viceversa a destra.
Voilà, siamo alla fine di questa seconda parte. Siamo già avanti ma restano ancora non poche cose da digerire. Nella prossima (la terza) tratteremo dell'umidità dell'atmosfera e della sua influenza sullo sviluppo dei cumuli. Parleremo anche, infine, delle curve adiabatiche. A presto, dunque, per le nuove avventure nel campo della comprensione dell'aerologia.
III parte
Nella seconda parte, abbiamo confrontato un emagramma ortogonale e un emagramma non ortogonale. Abbiamo parlato delle curve di stato dell'atmosfera che la rappresentano in un dato luogo, in un dato momento. Abbiamo infine soprattutto parlato della curva di temperatura, della fascia convettiva e dell'influenza del gradiente di temperatura sullo spessore di questa fascia.
Prima di continuare, ritengo necessario ripassare le nozioni fondamentali, e forse noiose, in merito all'umidità dell'aria. L'aria contiene sempre un po' di vapor d'acqua, anche se è bel tempo. Il vapor d'acqua è, dunque, acqua allo stato gassoso ed è incolore, perfettamente trasparente come l'aria secca, inodore ed insapore. Una nube o della nebbia, nettamente meno trasparenti, non sono vapor d'acqua, anche se ne contengono un po'. Una nube è un ammasso di acqua liquida in piccole (microscopiche) e innumerevoli goccioline d'acqua in sospensione in una porzione d'aria, come della polvere "d'acqua". Per dire il vero, ad esempio, non si dovrà dire della sauna che è un bagno di vapore ma piuttosto un bagno di nube calda. L'umidità dell'aria è un modo per dire che l'aria contiene una certa quantità di vapor d'acqua (e non nuvole). Non è facile capire l'umidità dell'aria poiché l'uomo non è dotato di un senso che possa avvertirla. Si dice vagamente che un'aria umida e calda è afosa e pesante. L'aria è satura di vapor d'acqua quando ogni quantità supplementare di vapore acqueo aggiuntale si trasforma in acqua liquida (appannamento, condensazione, nube, rugiada...). Più l'aria è calda e più può contenere una quantità massima (a saturazione) di vapor d'acqua. Per esempio, 1 m3 d'aria al suolo può contenere al massimo circa 32g d'acqua (sotto forma di vapore) a 30°C, 16g a 20°C, 8g a 10°C, 4g a 0°C, 2g a -10°C e 1g a -20°C. Avrete notato che ad ogni decina di °C raddoppia la quantità massima di vapore acqueo. La relazione non è dunque lineare ma esponenziale.
Esistono molto modi di misurare l'umidità. Per non logorarsi il fegato affronterò solo uno di questi, quello utile alla comprensione dell'emagramma. Poiché un'aria fredda può contenere meno vapore acqueo a saturazione che un'aria più calda, è sufficiente abbassare la temperatura di una massa d'aria per far apparire la rugiada, in parole povere la saturazione di questa massa in vapore. La temperatura (in °C) del punto di rugiada di una massa d'aria è, quindi, la temperatura alla quale bisogna portare questa massa d'aria perché risulti satura in vapor d'acqua e inizi a comparire la condensa (acqua liquida). Una massa d'aria a 20°C che ha un'umidità (=una temperatura del punto di rugiada) di 18°C è piuttosto umida, visto che basta un piccolo abbassamento della temperatura per saturarla di vapore d'acqua. Se il punto di rugiada è uguale a 2°C, si tratta invece d'aria piuttosto secca. Ancora una piccola precisazione: la temperatura del punti di rugiada non può essere, chiaramente, mai superiore alla temperatura; se la temperatura abbassa ancora, si ha condensazione supplementare e la temperatura del punto di rugiada segue parallelamente.
Torniamo all'emagramma ed al "temp". Poiché si può descrivere la struttura termica verticale dell'atmosfera utilizzando una curva di temperatura riportata sull'emagramma, si può fare la stessa cosa con la struttura verticale della sua umidità sotto forma di una curva di temperatura del punto di rugiada. La figura 1 mostra a destra la curva di temperatura (a) e a sinistra la curva d'umidità (temperatura del punto di rugiada) (b).
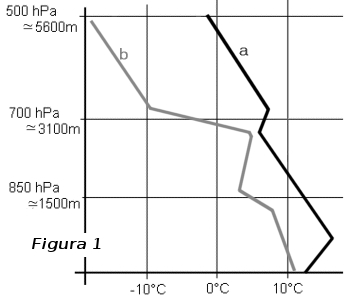
Si può notare sulla figura 1 che la separazione tra la curva della temperatura (a) e quella dell'umidità (b) è media verso 1500m, piccola verso 3000m ed elevata al di sopra. Questa distanza orizzontale è indicata in gergo meteo con il termine anglosassone "spread". Questo "spread" è espresso in °C poiché le due curve sono in °C. Osservate la fig. 1. Verso 1500m (850hPa), abbiamo uno spread di circa 7°C (=umidità media), verso 3000m (inversione di temperatura, curva a) abbiamo uno spread di circa 2°C (=umidità forte) e più in alto uno spread di oltre 15°C (=aria secca). Si ha d'altronde spesso una fascia d'aria umida a livello di un'inversione e dell'aria secca sopra di questa.
Abbiamo visto che la curva di temperatura è utile per stimare la qualità delle ascendenze termiche. A cosa può dunque servire la curva d'umidità? Bene, alla stima della nuvolosità. Come prima regola, più l'aria è umida e più la probabilità di formazione di nubi è grande. Seconda regola: l'altezza della base dei cumuli dipende dall'umidità al suolo. E' logico poiché l'aria delle termiche, responsabili dei cumuli, proviene dal suolo. Un'aria umida al suolo comporta una base delle nubi poco alta, e viceversa nel caso in cui l'aria al suolo sia secca. L'aria molto secca al suolo può dar vita a termiche blu. Terza regola: la quantità e lo sviluppo di nubi dipende dall'umidità in quota. Una forte umidità in quota comporta un sovrasviluppo di cumuli e viceversa. Nuovamente, aria molto secca può dar vita a termiche blu. Vediamo qualche esempio pratico (fig. 2).
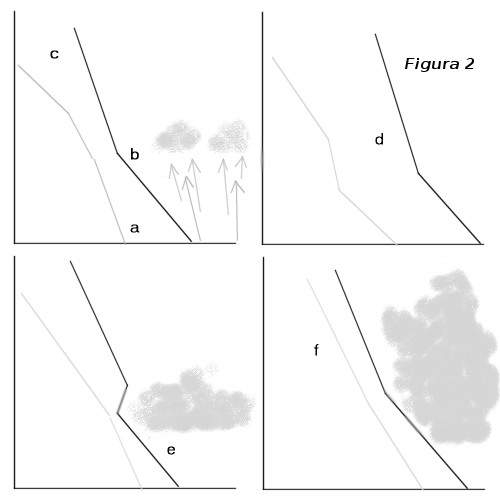
Nel grafico in alto a sinistra abbiamo aria poco umida al suolo (a), mediamente umida alle medie altitudini (b) e secca in alta quota (c). E' il caso della figura ideale. Si potrà incontrare qualche simpatico cumulo durante il volo, senza sovrasviluppo. Nel grafico di destra (d) l'aria è secca a tutte le quote. Ci sono poche chance di incontrare cumuli, soprattutto se il gradiente di temperatura è debole alle altitudini medie. In (e) l'atmosfera è piuttosto umida alle basse e media altitudini. Si rischia fortemente di trovare stratocumuli numerosi a sovrasviluppo orizzontale, soprattutto se c'è un'inversione termica. In (f) l'atmosfera è umida a tutte le quote. Si può prevedere un sovrasviluppo orizzontale e anche verticale, quindi temporali, soprattutto se il gradiente di temperatura è forte e non ci sono inversioni. L'aria è pesante e spesso brumosa. Per dare un'ordine di grandezza, il caso ideale potrà presentare uno spread leggermente superiore a 10°C nella fascia bassa, di circa 10°C alle medie altitudini (2000-4000m) e maggiore di 15°C in alta quota.
Poiché la temperatura del punto di rugiada non può essere superiore alla temperatura, la curva d'umidità è sempre a sinistra della curva della temperatura o, eventualmente, le due curve possono sovrapporsi, di solito parzialmente, se l'aria è molto umida (satura).
Siamo a buon punto. Per i minimalisti: se siete riusciti a seguire la spiegazione, le conoscenze acquisite dovrebbero già essere sufficienti per interpretare in maniera "basilare" un emagramma. Abbiamo visto come si presenta il grafico XY dell'emagramma e le curve di stato su questo disegnate. Queste curve di stato possono essere paragonate ad uno scatto fotografico (=immagine istantanea, bloccata) dello stato dell'atmosfera in un dato momento in un dato luogo. Su un emagramma esistono comunque 3 altre curve oblique. Si tratta di
- [(a)] curve adiabatiche secche,
- [(b)] curve adiabatiche umide,
- [(c)] curve del rapporto di mescolanza.
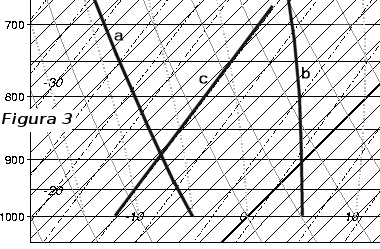
Su questa figura, solo un esemplare di ciascun tipo di curva è stato tracciato in grassetto, ma potete vedere le altre, grosso modo parallele. Le adiabatiche sono leggermente curve. La curva adiabatica secca (a) varia di un po' di meno di 1°C ogni 100m. La curva adiabatica umida (b) varia di circa 0,6°C ogni 100m. La curva del rapporto di mescolanza (c), che rappresenta l'evoluzione dell'umidità d'una massa d'aria ascendente, varia di circa 0.2°C ogni 100m. Provate anche a trovare ed evidenziare le isoterme, per esempio l'isoterma 0°C in grassetto. Nella IV parte, vedremo a che corrispondono e a che servono queste curve.
IV parte
Nella III parte abbiamo parlato dell'umidità dell'atmosfera, in particolare della curva di stato delle temperature del punto di rugiada e della sua influenza sulla nuvolosità cumuliforme. Abbiamo finalmente affrontato le curve dinamiche (per contrapposizione alle curve di stato, statiche) dell'emagramma: curve adiabatiche secca e umida, curva del rapporto di mescolanza. Andiamo ad addentrarci un po' di più in queste ultime curve.
Per restare fedeli alle nostri abitudini, un breve richiamo di fisica elementare in merito alla termodinamica dell'atmosfera. L'aria che si comprime (aumenta di pressione) si scalda e una massa d'aria che si dilata (diminuisce di pressione) si raffredda. Se questo cambiamento di temperatura ha luogo senza scambio di calore con l'aria circostante si parla di riscaldamento, o raffreddamento, adiabatico. In pratica si considera effettivamente che una massa d'aria in movimento nell'atmosfera non scambia quasi per niente energia (calore) con l'aria circostante, come se fosse racchiusa in una fine membrana da aerostato. Una massa d'aria in movimento verticale subisce, dunque, una trasformazione adiabatica. Se questa sale la sua pressione diminuisce (per adattamento alla pressione dell'aria circostante), si dilata e si raffredda (la sua temperatura diminuisce), senza perdere né acquisire del calore a favore/danno dell'aria circostante. Se invece scende la sua pressione aumenta, si comprime e si riscalda (la sua temperatura aumenta), senza fornire né togliere calore all'aria circostante. Questo aumento e diminuzione di temperatura si verificano in maniera precisa e sempre identica, qualsiasi sia la curva di stato della temperatura dell'aria circostante. Quando la massa d'aria è non satura in vapore acqueo, questa si raffredda (salendo) e si riscalda (discendendo) di 1°C ogni 100m (10°C ogni 1000m); si parla di trasformazione (o di curva) adiabatica "secca". Quando questa massa d'aria è satura in vapor d'acqua (aria in nube) questa si raffredda (salendo) e si riscalda (scendendo) di 0,6°C ogni 100m (3°C ogni 500m o 6°C ogni 1000m); si parla allora di trasformazione (o curva) adiabatica "umida" (detta anche "satura"). Vedi fig. 1
Perché queste differenze tra le due curve, "secca" e "umida"? Per evaporare (trasformazione da liquido a vapore), l'acqua ha bisogno di molta energia. Ne prende quindi dall'aria adiacente, è facile da spiegare: se si vuole far evaporare rapidamente l'acqua da una pentola c'è bisogno di riscaldarla. Il fenomeno inverso è più difficile da capire: quando il vapore acqueo si condensa (trasformazione da vapore a liquido) l'acqua (fini goccioline di nube) restituisce l'energia immagazzinata all'aria adiacente. Diremo quindi che, a temperatura identica, una massa d'aria umida contiene più energia liberabile (chiamata energia potenziale) di quanta ne contenga una massa d'aria secca. Si può capire così perché una massa d'aria umida sarà potenzialmente più instabile di una massa d'aria secca.
Quando una massa d'aria satura in vapor d'acqua sale o scende, va rispettivamente a raffreddarsi o riscaldarsi, quindi a far condensare o far evaporare dell'acqua, quindi a guadagnare o perdere dell'energia sotto forma di calore. In questo caso la curva adiabatica non è una vera adiabatica poiché c'è uno scambio di energia all'interno della massa d'aria in movimento verticale. Ma non c'è scambio di energia con l'aria atmosferica "immobile" più lontana. Salendo e ritrovando, attraverso la condensazione, del calore, la massa d'aria satura di vapore acqueo va così a raffreddarsi più lentamente che una massa d'aria non satura di vapor d'acqua, poiché quest'ultima non subirà il fenomeno della condensazione, liberatore di calore. Al contrario, in discesa e perdendo, per evaporazione, del calore la massa d'aria satura di vapore acqueo si riscalderà meno velocemente di una massa d'aria non satura, poiché quest'ultima non subirà il fenomeno dell'evaporazione, "ladro" di calore. E' quindi a causa dei fenomeni di evaporazione e condensazione che c'è differenza tra le curve adiabatiche secca e umida.
La terza curva importante è quella del rapporto di mescolanza. In pratica bisogna semplicemente ritenere che c'è una retta che mostra l'evoluzione dell'umidità d'una bolla d'aria che sale. Il suo gradiente vale -0,2°C ogni 100m. Esempio: se l'umidità (in temperatura del punto di rugiada) di una bolla d'aria originata al suolo vale 10°C, l'umidità di questa bolla a 1000m sopra al suolo sarà di 10 - 1000*0.2/100 = 8°C.
Vediamo queste trasformazioni adiabatiche ed il rapporto di mescolanza tracciati sull'emagramma. Vedi fig. 2
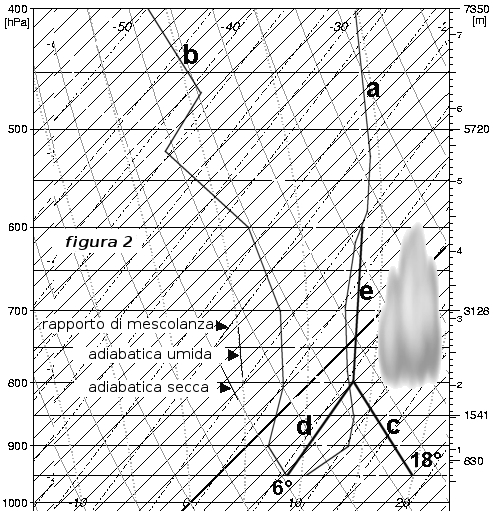
Le curve a e b rappresentano rispettivamente le curve di stato di temperatura e di umidità in °C. Al suolo si misura un'umidità di 6°C e si prevede una temperatura (bollettino meteo) massima di 18°C. Assumiamo, per semplicità, che si tratti di una situazione meteo che non subisce variazioni nell'arco della giornata. Ciò significa che la temperatura in quota e la curva di umidità non cambieranno in maniera significativa. Grazie al sole, al riscaldamento del suolo che provoca a sua volta un riscaldamento progressivo della bassa atmosfera per convezione, la curva di stato di temperatura parte da 18°C al suolo (temperatura massima, al centro del pomeriggio) per seguire più in alto la curva adiabatica secca in c (fig. 2). Questa curva va finalmente ad incontrare la curva di temperatura del mattino verso i 2000m (800hPa). Di conseguenza, la curva di stato di temperatura del pomeriggio va ad essere composta da c (suolo-2000m) e da a (da 2000 in su).
Vedremo più avanti che a partire da 200-300m dal suolo, la temperatura delle bolle termiche ascendenti è molto prossima a c. Se una bolla termica sale partendo dal suolo, la sua umidità decresce di 0,2°C/100m (rapporto di mescolanza) a partire da 6°C (vedi curva b della fig. 2). Le curve c e d finiscono così per incrociarsi verso 2000m. In altre parole, a questa quota, la temperatura e la temperatura del punto di rugiada (umidità) sono identiche nelle bolle termiche (non nell'atmosfera libera vicina). Ciò significa che l'aria della bolla diventa satura in vapor d'acqua, e questo provoca una condensazione quindi la formazione di nubi di convezione. E' a questa quota che si troverà la base dei cumuli. E' dunque l'umidità al suolo che determina la base delle nubi, come abbiamo visto nel precedente articolo. La bolla termica continuerà a salire finché la sua temperatura sarà superiore a quella dell'aria circostante. Poiché ora abbiamo condensazione, l'aria si raffredderà non di 1°C/100m (adiabatica secca) ma di un valore compreso tra 0,5 e 0,8°C/100m (questo gradiente varia in funzione della quota e della temperatura dell'aria circostante). Si parla allora di adiabatica umida. La bolla si raffredda quindi meno velocemente (vedere curva e della fig. 2) salendo e potrà raggiungere una quota maggiore che se fosse restata secca. Da quando la curva incrocia la curva di temperatura, la bolla termica cessa di salire. Esiste anche un altro fenomeno che blocca lo sviluppo verticale delle nubi di convezione. In effetti se l'atmosfera è molto secca in quota (se la temperatura del punto di rugiada è molto lontana, più di 15-20°C, della temperatura; a quota identica) questa limita sicuramente il sovrasviluppo nuvoloso e l'ascendenza d'aria associata.
Vi suggerisco ora di riprendere e di rileggere gli articolo precedenti. In principio avrete compreso l'essenziale del funzionamento dell'emagramma. Devo comunque e purtroppo riconoscere, a rischio del vostro dispiacere, che in pratica nelle nostre regioni caratterizzate da forti variazioni topografiche, climatiche e meteorologiche l'utilizzo del radiosondaggio di Payerne della notte precedente e la tracciatura delle curve della figura 2 si riveleranno molto spesso completamente inesatte e, dunque, inutilizzabili per una previsione affidabile del giorno. Vedremo nei prossimi articoli il perché e soprattutto come rimediare grazie ai modelli numerici, disponibili attualmente su internet, e alla conoscenza dei particolari topografici delle nostre zone. Tutto ciò che abbiamo fatto fino ad ora è comunque essenziale per comprendere ciò che succede verticalmente nell'atmosfera. Con un po' d'abitudine si possono fare delle previsioni al primo colpo d'occhio con l'aiuto delle curve di temperatura e d'umidità previste dai modelli numerici, senza dover disegnare laboriosamente tutte queste adiabatiche.
V parte
Fino ad ora abbiamo visto l'essenziale dell'interpretazione degli emagrammi e delle curve di stato. Lo scopo era di comprendere il principio pratico del dinamismo termo-convettivo atmosferico su un terreno omogeneo e piatto o poco accidentato. Nelle nostre zone, a causa della meteo capricciosa e soprattutto della varietà morfologica del terreno (colline, laghi, pianure, valli, alte montagne), l'applicazione tale e quale di questi principî al radiosondaggio della notte precedente il giorno del volo si rivela molto raramente attendibile e dà più spesso risultati disastrosi e falsi. Questo è dovuto principalmente a due fatti: Il riscaldamento e il dinamismo termo-convettivo dell'atmosfera sono totalmente differenti a seconda della forma e della natura della superficie terrestre sottostante. Per la stessa situazione meteo, le curve di stato sono molto differenti sopra un lago rispetto a dentro ad una stretta e alta valle alpina. Più spesso la situazione meteo varia in maniera significativa dal centro della notte, quando vengono effettuate le rilevazioni del radiosondaggio, al centro della giornata seguente, momento in cui ha luogo il volo. Ciò significa che le curve di stato, fatti da parte i cambiamenti convettivi abituali della bassa atmosfera, possono essere significativamente differenti tra la notte ed il giorno seguente. Ad esempio, l'atmosfera può in qualche ora umidificarsi o, al contrario, seccarsi oppure, a causa dei fenomeni convettivi, può globalmente riscaldarsi o raffreddarsi.
Influenza del cambiamento della situazione meteorologica sul riscaldamento convettivo delle fasce basse
Guardare la fig. 1. Dovreste riconoscere un riscaldamento puramente convettivo della bassa atmosfera tra la curva di stato di temperatura delle 3h00 del mattino e quella delle 15h00 del pomeriggio seguente.
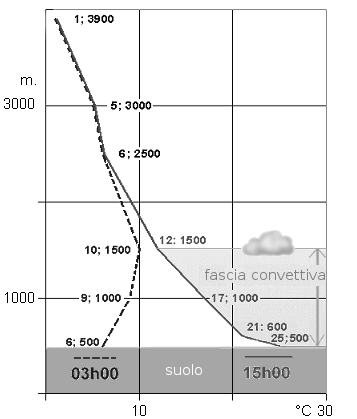
Verso le 3h00 del mattino, l'atmosfera presenta una struttura termica rappresentata dalla curva tratteggiata con l'inversione termica al suolo, da 500m a 1500m circa, e più in alto un gradiente di temperatura di circa 0,4-0,5°C/100m. Verso le 15h00 la temperatura dell'aria vicina al suolo raggiunge il suo massimo, per esempio circa 25°C. Più in alto, qualche decina di metri più in su, la temperatura decresce molto rapidamente, di oltre 1°C/100m (gradiente sovradiabatico). Ancora più in alto, fino a 1500m circa, possiamo notare un gradiente termico adiabatico di 1°C/100m. E' logico poiché in questa fascia si trovano movimenti convettivi verticali incessanti. In effetti si ricorderà che una massa d'aria in movimento verticale si riscalda o si raffredda di 1°C ogni 100m. E' solo all'interno di questa fascia che si troveranno i movimenti convettivi secchi. Sopra la fascia convettiva, con o senza isotermia o inversione, il gradiente termico varia abitualmente tra 0,3°C e 0,8°C ogni 100m. Abbiamo già visto rapidamente, e lo rivedremo ancora più avanti, che più quest'ultimo gradiente termico è alto, più la fascia convettiva sarà spessa, migliori saranno le ascendenza termiche.
Si vede comunque bene che l'esercizio grafico della figura 1 non può essere variabile se la situazione meteorologica non varia del tutto dalla notte al giorno seguente, cosa assai rara da noi. Sulla fig. 1, l'atmosfera non si riscalda in corso della giornata se non nelle sue fasce basse attraverso i fenomeni convettivi (il suolo riscaldato dal sole, poi l'aria sovrastante riscaldata per convezione verticale). Ma nella maggior parte dei casi l'atmosfera globalmente si riscalda o si raffredda, più o meno sensibilmente, dalla notte in cui è stato fatto il radiosondaggio alla giornata di volo seguente per motivi diversi dalla convezione. Non si può dunque affidarsi ciecamente al radiosondaggio della vigilia per prevedere la qualità delle ascendenze termiche.
Ci sono due fenomeni che sono all'origine di un cambiamento di temperatura non convettivo: i movimenti orizzontali dell'atmosfera chiamati avvezioni (avvezione d'aria fredda o d'aria calda) che raffredda o riscalda l'atmosfera alla quota dove questa si verifica; i lenti movimenti verticali e globali non convettivi dell'atmosfera su una regione molto ampia. Se si tratta di movimenti discendenti (di caduta lenta e generalizzata che insiste su un'ampia zona) si parla di subsidenza. Nei forti anticicloni si trova generalmente questa subsidenza. Se, al contrario, si tratta di un lento movimento ascensionale si parla di antisubsidenza, che si trova generalmente nelle zone di bassa pressione. E' importante non confondere i movimenti atmosferici verticali di subsidenza-antisubsidenza e i movimenti atmosferici verticali termoconvettivi. Vedere fig. 2. A sinistra, abbiamo un movimento di subsidenza lenta (c), che si estende su un'ampia regione e si produce sopra la fascia convettiva (b), questa a contatto col suolo (a), dove hanno luogo l'uno accanto all'altro i movimenti verticali termici, ascendenti e discendenti, più rapidi e più stretti. Viceversa, a destra, sopra una fascia convettiva più spessa e più attiva, si verifica un fenomeno di antisubsidenza (d). Come ordine di grandezza, la velocità verticali di subsidenza e antisubsidenza è di qualche decina di metri al giorno!
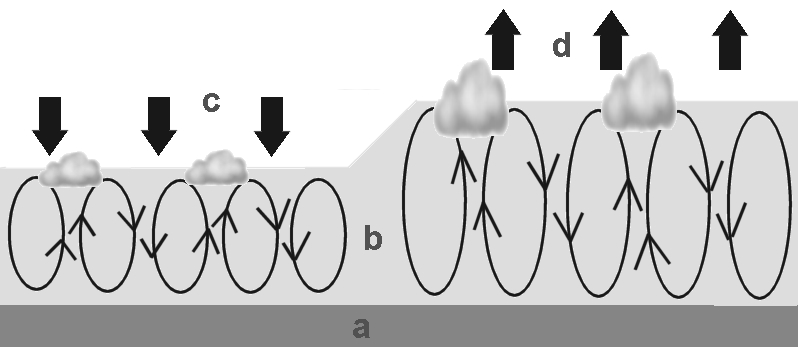
figura 2
Come agisce la subsidenza? semplicemente in un riscaldamento della media atmosfera. Nella figura 3, si riprende l'esempio della figura 1 ma con una componente di subsidenza a quota media, mettiamo da 2000 a 4000m. La particella d'aria si trova durante la notte al punto P e si trova più bassa durante la giornata, al punto P'. Questa particella d'aria subisce dunque, attraverso il suo movimento verticale discendente, un riscaldamento adiabatico (1°C/100m).
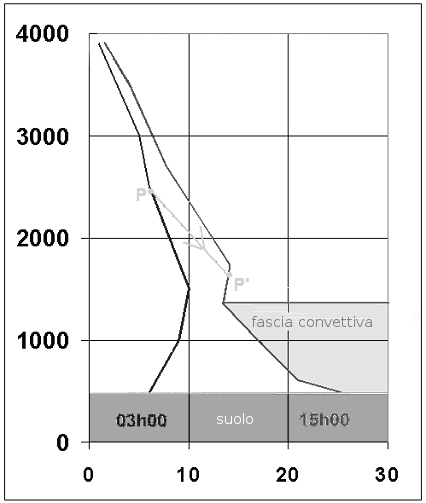
figura 3
Se si fa lo stesso ragionamento per l'esempio della curva della notte, si comprende come si ottiene una curva inclinata verso destra, quindi più calda, alle medie altitudini, nel pomeriggio e un'inversione verso 1300m. Si nota allora, confrontando le due figure 1 e 3, che la fascia convettiva sulla figura 3 è più sottile quindi meno buona per le ascendenze che sulla figura 1. Parallelamente la subsidenza comporta anche un essiccamento dell'atmosfera al suo livello. Vedere la fig. 4. Al di sopra dei 1500m (inversione dovuta alla subsidenza) la curva d'umidità, in temperatura del punto di rugiada, si allontana in effetti notevolmente dalla curva di temperatura.
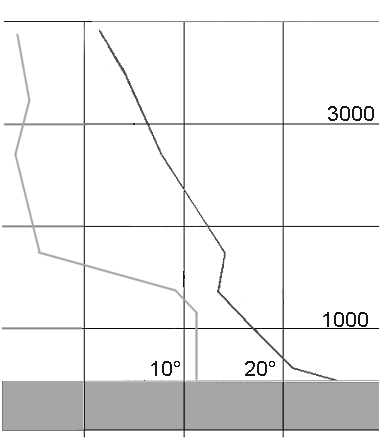
figura 4
Un'avvezione d'aria calda alle medie altitudini può causare la stessa evoluzione delle curve di stato di temperatura che sulla figura 3.
Al contrario, attraverso il fenomeno inverso, l'avvezione di aria fredda alle medie altitudini e l'antisubsidenza comportano un raffreddamento dell'atmosfera come raffigurato attraverso l'evoluzione delle curve di temperature della figura 5.
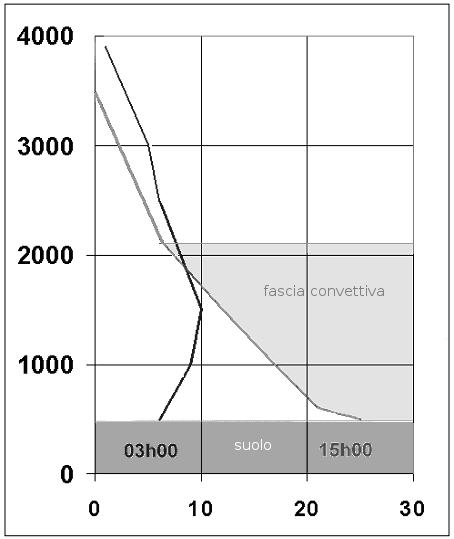
figura 5
Questo raffreddamento s'accompagna ad un aumento dello spessore della fascia convettiva, quindi della qualità delle ascendenze termiche, ma anche spesso, purtroppo, ad un aumento dell'umidità (rischio accresciuto di sovrasviluppo nuvoloso e di temporali).
Riassumendo, l'avvezione d'aria calda o la subsidenza nelle fasce medie dell'atmosfera possono abbassare il limite superiore della fascia convettiva (che comporta una diminuzione della qualità delle termiche); invece l'avvezione d'aria fredda e l'antisubsidenza possono, al contrario, alzarlo (il che può comportare un miglioramento della qualità delle termiche ma anche, purtroppo, un aumento dell'umidità dell'aria, della nuvolosità e dei temporali).
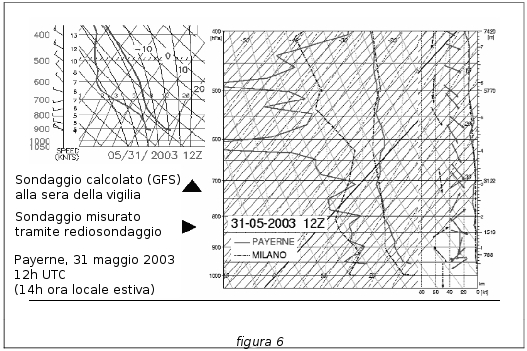
Ad ogni modo, vista l'evoluzione sempre possibile della situazione meteo generale, tutti avranno compreso perché non si può utilizzare le curve del radiosondaggio della notte precedente per fare previsioni affidabili delle ascendenze termiche e dei cumuli (altezza e quantità) che ci saranno durante il pomeriggio seguente. Allora come fare? Ebbene, attualmente, grazie all'informatica e ad internet, abbiamo per questo molte possibilità. Dopo diversi anni, i migliori ricercatori in meteorologia hanno messo a punto con successo delle logiche molto sofisticate utilizzando dei calcolatori molto potenti che calcolano ogni giorno, su qualche giorno, l'evoluzione dei differenti parametri atmosferici (pressione, temperatura, umidità, venti, etc) del mondo intero a partire dai parametri atmosferici misurati nel mondo intero. Molti di questi modelli sono disponibili su internet. Il più completo e, secondo me, il migliore è il modello americano GFS (Global Forecast System), precedentemente AVN e MRF. Sul mio sito personale (www.soaringmeteo.com) ho inserito qualche accesso facilitato a questo modello che richiede, comunque, una certa interazione (quindi una certa intelligenza) all'utilizzatore. Su questa pagina web ho inserito qualche lista di diversi indirizzi di volo con le relative coordinate geografiche. A partire da là, seguendo le diverse istruzioni, potete ottenere un emagramma ("sounding") calcolato (previsto) per la data e il luogo che vi interessa. La figura 6 offre un raffronto tra il sondaggio calcolato (alla sera della vigilia) e un sondaggio rilevato alla stessa ora e data al di sopra di Payerne. Si nota logicamente che la curva calcolata è più liscia ed offre una tendenza generale dell'atmosfera e che il sondaggio rilevato contiene più dettagli ma, in sostanza, più ingombranti che utili. Nel complesso i due sondaggi si rassomigliano notevolmente. L'ho notato spesso, in 2-3 anni d'utilizzo intensivo. Si nota tramite entrambi i sondaggi, un'umidità assai pronunciata nelle fascia basse e molto leggera tra 700 e 500hPa (circa 3000 e 5500m), un'isoterma di 0°C verso 650hPa (circa 3700m), un gradiente termico di circa 0,6°C/100m tra 2000 e 4000m e dei venti piuttosto deboli di tendenza da W a NW in quota. Il radiosondaggio della notte mostra un'umidità più forte verso 3000-4000m e dei venti variabili.
Vedremo in un prossimo articolo come interpretare il meglio possibile un sondaggio previsto evidenziando quali sono gli inganni da evitare. Abbiamo, in ogni caso, visto che è meglio affidarsi al sondaggio calcolato e previsto dai modelli numerici che al radiosondaggio effettuato alla vigilia. I modelli numerici fanno dunque miliardi di calcoli in un tempo relativamente breve per mostrarci come andranno evolvendo, su qualche giorno, i venti, le temperature e l'umidità dell'atmosfera nel mondo intero, a differenti altitudini e tengono quindi conto, molto meglio della stima approssimativa di un essere umano, di avvezione, subsidenza, convezione e altri fenomeni termodinamici.
Influenza della topografia sulla fascia convettiva
La figura 1 mostra l'evoluzione delle curve di stato di temperatura su una superficie terrestre relativamente omogenea e poco accidentata (piana) in occasione di una situazione meteo stabile (poco variabile).
La topografia sottostante influenza comunque molto fortemente la fascia convettiva e la relativa struttura termica. Prendiamo 4 esempi: il Pateau Svizzero, il litorale dei grandi laghi, le valli alpine larghe e basse, le valli alpine alte e strette. A pari gradiente termico (tra 1000 e 3000m sopra dei litorali e del Plateau e tra 2000 e 4000m per le Alpi), la fascia convettiva è più spessa nelle Alpi (riscaldamento molto efficace di un piccolo volume d'aria imprigionato dentro le valli), meno
Vediamo ciò con le curve delle temperature. Le curve di stato della figura 7 sono un esempio di ciò che può accadere durante una bella giornata estiva e mostrano una fascia convettiva (gradiente di 1°C/100m) di 300m circa di spessore per le coste lacustri, 1000m circa per il Plateau e 1600m circa per una valle alpina. L'avvezione fredda, dovuta alla potente brezza di valle, nella parte inferiore delle grandi valli comporta a mezza altezza una fascia non adiabatica in cui le convezioni sono bloccate. Sopra i 3000m le temperature sono assai simili qualunque sia la regione, durante una situazione meteo omogenea su tutta la svizzera montagnosa o no (per esempio anticiclone).
Fino ad ora abbiamo visto pressoché tutto sulla struttura termica dell'atmosfera, come questa evolve e con quali strumenti possiamo prevedere la sua evoluzione; com'è influenzata dalla topografia sottostante, tanto variabile nelle nostre zone. Nel prossimo articolo e grazie alla competenza acquisita fino ad ora, potrò infine insegnarvi qualche piccolo trucco pratico per fare le vostre previsioni, come dei professionisti (...meglio se possibile, perché bisogna dire che Météosuisse non è sempre brillante....;-)). Nei prossimi articoli approfondiremo ancora un po' la nozione di fascia convettiva, per meglio comprenderne l'importanza, e la struttura delle ascendenze termiche.
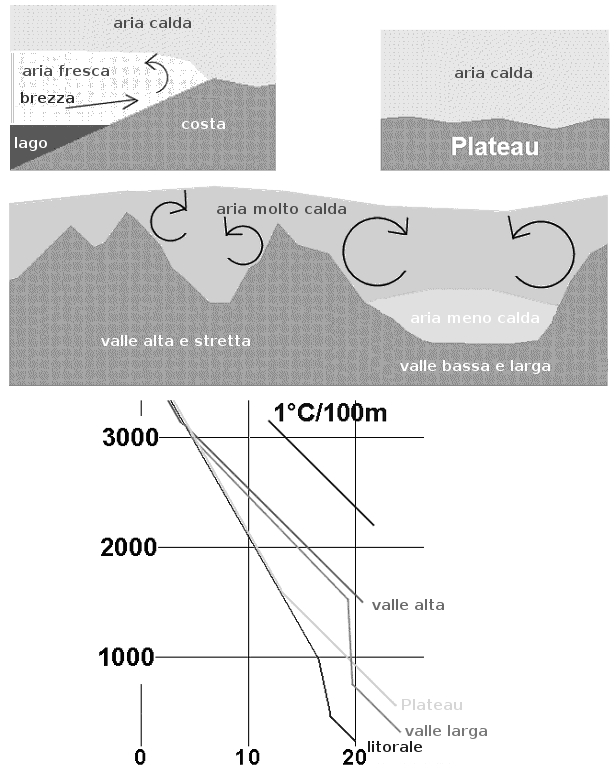
figura 7
VI parte
Negli articoli precedenti abbiamo visto tutti i fondamenti ed i principî del riscaldamento convettivo dell'atmosfera oltre che l'influenza della curva d'umidità sull'altezza e la quantità delle nubi. Abbiamo anche visto l'utilizzo teorico ma poco pratico dell'emagramma. Ho inoltre insistito sull'assurdità di voler utilizzare i radiosondaggi misurati la notte precedente per fare previsioni sulle termiche.
Allora, come fare in pratica? Tutti gli strumenti si trovano sul mio sito web:
- [www.soaringmeteo.com]
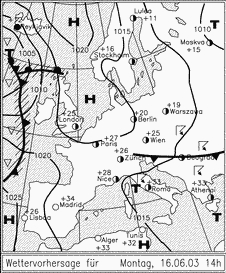
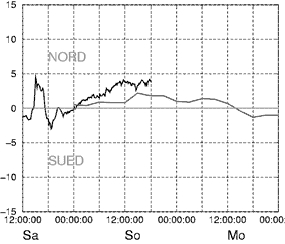
figura 1
E' dunque la giornata di lunedì che bisogna investigare più a fondo. Se si fossero previsti venti forti, una differenza di pressione transalpina importante (più di 3 o 4hPa) o una nuvolosità importante, mi sarei fermato a questo punto. Ma siccome questo lunedì può essere potenzialmente buono per un volo di distanza nella Alpi, ho continuato l'analisi meteo. Bisogna cliccare anche sul link (collegamento) "modèle numérique", dopodiché scegliere il luogo di previsione. Io sono solito scegliere Payerne per le Alpi (non mi dilungherò sul perché di questa scelta per non appesantire il testo). La pagina seguente offre la scelta del modello numerico ed il tipo di rappresentazione. Scegliamo "sounding, GFS 0-84h" che significa: modello GFS, il più preciso, in modalità sondaggio previsto. La pagina successiva ci chiede di selezionare la data di nostro interesse, in questo caso il 16 giugno 2003 alle 12h00UTC o 14h00 ora locale (estate). Finalmente si ottiene il grafico della figura 2 che è l'emagramma previsto per il periodo di volo scelto (alle 12UTC, 14 ora locale), sopra a Payerne. Ritroviamo a destra il profilo dei venti alle differenti altitudini. Si prevede quindi vento debole (4-10km/h) da nord verso 2000-3500m. In realtà il vento da Nord e la sovrappresione nord sono stati un po' più forti di quanto previsto, il che non ha impedito a qualche pilota di fare oltre 100km nella Haut Valais. Al centro, si trova l'emagramma propriamente detto con la curva di temperatura a destra e la curva d'umidità a sinistra.
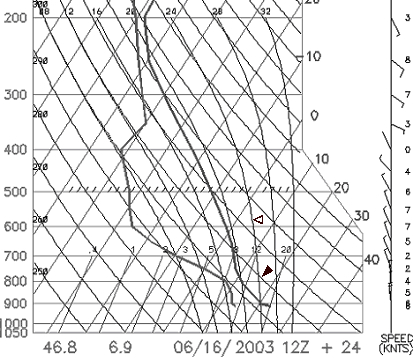
figura 2
Si può notare che verso 200-300hPa (9000-12000m di altitudine) le due curve sono molto vicine con una differenza, o "spread", di circa 4-5°C. Uno spread inferiore a questi valori comporta, invece, un alto rischio di formazione di nuvolosità alta di tipo Cirrostratus. Più basso, verso 400-600hPa (4000-8000m), le due curve sono molto lontane l'una dall'altra (spread tra 25 e 30°C). E' eccellente. Questo eviterà ogni sovrasviluppo nuvoloso orizzontale (altocumulus) e verticale (cumulonimbus). Infine, alle fasce basse, verso 800-850hPa (1500-2000m), l'atmosfera ritorna umida (spread di circa 5°C). Ciò lascia supporre che la base dei cumuli non sarà molto elevata. Se si osserva ora, sempre nella fig. 2, la curva di temperatura (curva destra) tra 900 e 600hPa (1000-4000m), si riconoscerà facilmente tra 900 e 800hPa la fascia convettiva con la sua curva parallela alle adiabatiche secche (1°C/100m, freccia piena). Al disopra della fascia convettiva, la curva di temperatura è pressoché parallela alla curva adiabatica umida (circa 0,6°C/100m, freccia vuota).
Per meglio comprendere cosa succede nelle basse fasce atmosferiche, nostre altitudini di volo, prendiamo un ingrandimento dell'emagramma relativo a questa parte d'atmosfera. Vedere la figura 3.
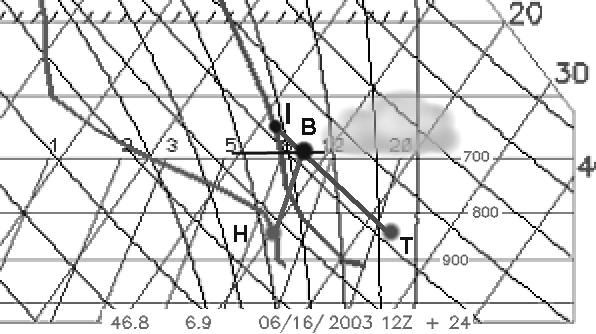
figura 3
Notiamo subito un fatto sorprendente. Le curve partono dall'altitudine 900hPa ossia circa 1000m, visto che Payerne si trova all'altitudine di 450m circa. Ciò è dovuto al fatto che il modello numerico GFS, attraverso le sue maglie di 100km, vede le Alpi e la Jura come un'enorme collina a pendio dolce, culminante verso il Gothard a 1500m. Le valli alpine ed il Plateau sono dunque "appiattite e riempite" cosicché, per il modello, la Jungfrau e Brig si trovano a circa 1500m, Sion verso 1300m, Payerne verso 1000m e la Jura verso 800m. Al suolo nei pressi di Payerne, verso 1000m o 900hPa per il modello, questo ha rappresentato una fine fascia atmosferica di sovradiabatismo attraverso un piccolo segmento quasi orizzontale all'inizio della curva di temperatura. Si ritrova quindi in pratica tutto ciò che ho spiegato negli articoli precedenti in merito al riscaldamento della bassa atmosfera.
Serve comunque fare attenzione ad una cosa. Poiché il modello non "vede" le valli alpine, né i bacini lacustri, né altre variazioni locali della nostra topografia tormentata, queste curve non rappresentano che una tendenza generale dell'atmosfera che va obbligatoriamente adattata alle condizioni topografiche reali e complesse del nostro paese per fare delle previsioni valide. Esempio pratico: il modello annuncia un piccolo vento da Nord vero i 2000m nella regione dell'Haut-Valais. Che pensate di trovare al decollo di Fiesch (pendio orientato a SE) verso le 11h00? Ebbene, un vento termico di pendio da SE!
Con la curva di temperatura questo adattamento è meno evidente! Nell'articolo precedente abbiamo visto che grazie al piccolo volume d'aria da riscaldare, l'aria delle valli alpine si riscalda di più e più in fretta. Bruno Neiniger, fisico atmosferico dell'EPFZ e volovelista, ha scoperto e documentato che la bassa atmosfera della valle di Conches (Goms) si riscalda circa 2 volte più in fretta e 2 volte più che sul Plateau, in estate. Gaudenz Truog, un altro meteorologo di Zurigo, ha dimostrato empiricamente che la temperatura massima a 1500m in una valle alpina si calcola semplicemente sottraendo 5°C alla temperatura massima prevista sul Plateau (a 500m di altitudine). In altre parole, se è stata prevista una temperatura massima di 28°C in Svizzera per il 16 giugno 2003, si può prevedere anche 23°C max a 1500m nelle valli alpine. Se si riporta questo valore sull'emagramma della figura 3, al punto T (3°C, 850hPa = 1500m circa), si può allora tirare un'adiabatica che parte da T fino alla sua intersezione in I con la curva di temperatura, verso 650hPa ovvero 3700m circa. Si poteva quindi prevedere per quel giorno la massima fascia convettiva alpina grosso modo da 1500 a 3700m.
Possiamo anche continuare con la previsione della base dei cumuli nelle Alpi per questo stesso giorno seguendo le regole degli articoli precedenti. Si parte da H, temperatura del punto di rugiada (umidità) a 850hPa. Si traccia una riga parallela alle curve del rapporto di mescolanza fino all'intersezione con la curva di temperatura in B. Se B si trova nella fascia convettiva avremo formazione di cumuli altrimenti avremo termiche blu. Per questo 16 giugno, B si trova a un po' più di 700hPa ovvero 3100m. Per le Hautes Alpes (Goms, Zermatt, Saas, Evolène) si può aggiungere da 300 a 500m. Neiniger ha anche determinato che se la sommità della fascia convettiva massima è sotto ai 3500m le ascendenze alpine saranno poco sfruttabili, in aliante ad ogni modo, per il volo di distanza. Per questo 16 giugno la sommità della fascia convettiva massima nelle Alpi è dunque prevista al disopra di 3500m.
Brevemente; dopo l'emagramma delle figure 2 e 3, tutto porta a credere che le condizioni di volo del 16 giugno saranno pressappoco ideali. In effetti, quel giorno, sono stai fatti diversi voli di 100km nell'Haut-Valais. Vi lascio inoltre ammirare, alla figura 4, l'aspetto del cielo verso mezzogiorno -ora locale- nel Goms. La base dei cumuli si trova effettivamente tra 3100 e 3600m.

figura 4
Per confronto, la figura 5 mostra l'emagramma della giornata del 19 giugno 2003. Facendo lo stesso ragionamento fatto in precedenza, il punto I si trova sotto dei 700hPa quindi verso 2900-3000m. La fascia convettiva alpina massima non era dunque spessa in quel giorno e che io sappia nessun volo di distanza alpino degno di questo nome è stato registrato nel server OLC-CCC. Per i migliori osservatori, si può spiegare la poca altitudine di I attraverso la differenza di temperatura tra 800 e 600hPa (2100 e 4400m circa) poco marcata, ovvero di circa 11°C che corrispondono ad un gradiente termico medio di 0,5°C/100m.
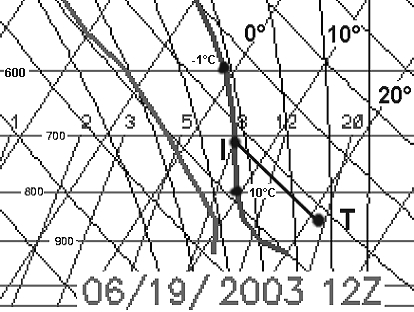
figura 5
A questo punto mi piace fornirvi un altro piccolo trucco per vedere al primo colpo d'occhio se il gradiente di temperatura è favorevole per le Alpi. Guardate la figura 6. Si tratta di confrontare la curva di stato di temperatura tra 800 e 600hPa con le curve adiabatiche umide (frecce) che rappresentano un gradiente di circa 0,6°C/100m. Se la curva di temperatura è meno inclinata sulla sinistra della curva adiabatica umida significa che il gradiente della curva di stato è minore di 0,6°C/100m. Questo, in linea di principio, non è favorevole (vedere figura a sinistra). Se, al contrario, la curva di temperatura è più inclinata a sinistra delle curve adiabatiche o è parallela a queste, significa che il gradiente della curva di stato è maggiore di 0,6°C/100m o uguale a questo valore; ciò è favorevole (vedere figura a destra).
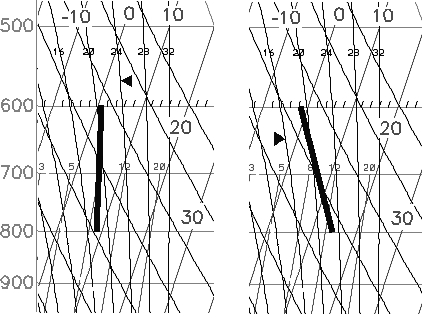
figura 6
Riassumendo: la previsione delle ascendenze termiche nelle Alpi sembra finalmente assai semplice ed immediata. In un primo momento si cerca la giornata soleggiata con venti e differenza di pressione deboli. In un secondo momento si studia più attentamente questa giornata attraverso l'emagramma previsto (modello GFS) per il centro della giornata. Su questo grafico ci sono tre parametri atmosferici ai quali bisogna prestare attenzione: il vento: bisogna studiare la direzione e l'intensità del vento alle varie quote l'umidità dell'aria alle differenti altitudini, tramite la quale ci possiamo fare un'idea sulla nuvolosità e sull'altezza della base dei cumuli la temperatura e più in specifico la differenza di temperatura tra 800 e 600hPa circa, con cui possiamo valutare lo spessore della fascia convettiva e, dunque, la qualità delle ascendenze nelle Alpi.
VII parte
Sappiamo adesso ben interpretare un emagramma sia esso sul Plateau che nelle Alpi. Abbiamo visto, allo stesso tempo, che è preferibile utilizzare, per le previsioni, le curve di stato previste durante la giornata di volo dai modelli numerici rispetto a quelle misurate la notte precedente attraverso il radiosondaggio. Abbiamo già parlato della fascia convettiva (fc). Mi piacerebbe ora approfondire un po' questa nozione per comprendere meglio, poi, la struttura di un'ascendenza termica.
Gli anglosassoni parlano di "convective boundary layer" o di "mixing boundary layer"; in parole povere una fascia troposferica limite (a contatto col suolo) nella quale si verificano intensi fenomeni di convezione e di rimescolamento d'aria (turbolenze e rotori). Questa si estende dal suolo fino ad una certa altitudine ed il suo spessore può variare da qualche decina di metri (in inverno nelle nostre zone) a qualche migliaia di metri (in estate nelle zone tropicali). E' unicamente dentro a questa fascia d'aria che si trovano le ascendenze termiche da noi sfruttabili. Poiché c'è un rimescolamento incessante d'aria a causa di turbolenze, rotori e movimenti verticali (ascendenti e discendenti) è una fascia generalmente un po' brumosa con un limite orizzontale superiore assai netto. Si riconosce bene questo limite allorché si arriva alla sommità dell'ascendenza. Vedere fig. 1. Le sommità dei cumuli si trovano frequentemente al disopra della fc poiché all'interno di questi il gradiente termico dell'aria in ascesa è inferiore a 1°C/100m (segue l'adiabatica umida, quindi 0,5-0,8°C).

figura 1
Nella fc, il gradiente termico è quasi identico a quello dell'adiabatica secca, quindi 1°C/100m. Logico poiché l'aria sale, scende e si mescola continuamente. Vicino al suolo surriscaldato, per qualche decina di metri, il gradiente è generalmente superiore a 1°C/100m. Si parla di gradiente sovradiabatico. Al di sopra della fc, il gradiente è inferiore a 0,8°C/100m. Non c'è obbligatoriamente un'inversione termica alla sommità della fc ma è chiaro che un'inversione significativa situata a 1000-1500m dal suolo (2500-3000m di altitudine sulle Alpi) comporta sicuramente un blocco della fc a quel livello. D'altra parte, più il gradiente termico al disopra della fc è elevato e più la sommità della fc sarà alta. Ciò racchiude le astuzie di previsione descritte negli articoli precedenti.
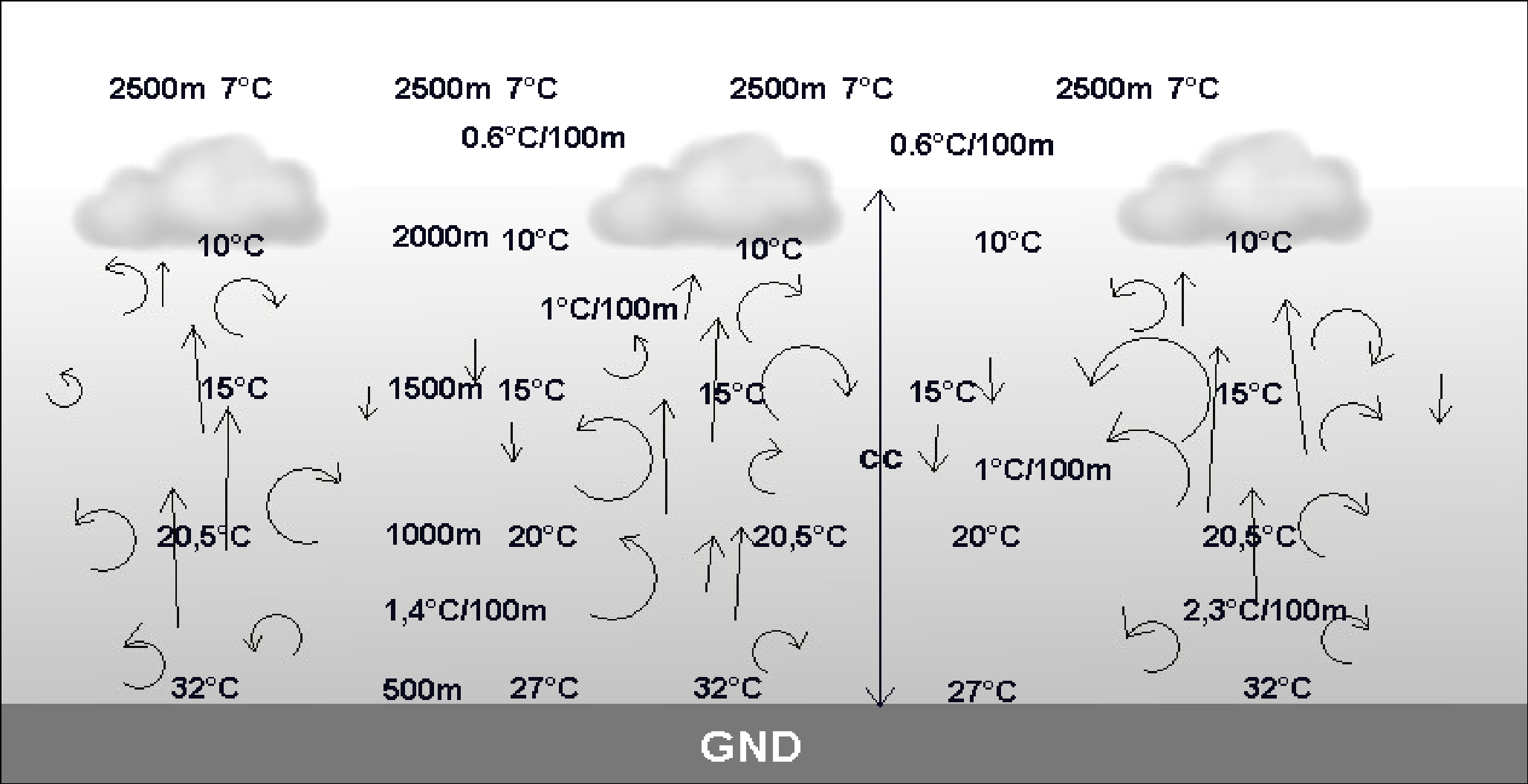
figura 2
La figura 2 mostra uno schema della fc. Si riconosce la sua estensione verticale dalla bruma grigia. Ho rappresentato i movimenti verticali e le turbolenze della fc utilizzando delle frecce. In questo esempio ho scelto una media di 27°C (temperatura dell'aria) al livello del suolo. Sulle superfici scure e secche si può immaginare di incontrare delle fasce d'aria a contatto col suolo che arrivano fino a 32°C. E' evidentemente in questo posto che si hanno più probabilità di incontrare ascendenze termiche. Se le differenze di temperatura dell'aria al suolo sono sensibili tra le sorgenti termiche e le altre zone del suolo, sono sorprendentemente nulle qualche centinaia di metri più in alto, come è stato dimostrato da un fisico e volovelista tedesco, Lindmann. Wallington, un fisico e volovelista australiano, pensa che sia il surplus di vapore acqueo, più leggero dell'aria secca, che assicura la salita della bolla termica fino a qualche centinaia di metri dal suolo. In effetti anche in una termica blu, in cui il punto di condensazione non viene mai raggiunto, l'umidità dentro l'ascendenza aumenta con l'altitudine secondo la linea del rapporto di mescolanza anche se nell'aria circostante l'umidità tende a diminuire. Nel mio esempio, simile al modello di Lindmann, non c'è che 0,5°C di differenza termica tra l'aria circostante e l'aria dell'ascendenza, 500m AGL (al disopra del suolo). Più in alto la differenza è quasi nulla. Dal suolo fino a 500m AGL il gradiente di temperatura è indubbiamente sovradiabatico poiché si passa da 27-32°C a 20-20,5°C. Più alto, fino a 2000m, il gradiente è adiabatico (10°C/1000m) e più in alto ancora, in cima alla fc, si ha un gradiente di 0,6°C/100m (3°C/500m). Una volta che la bolla termica ha lasciato il suolo, l'aria al suo interno si raffredda molto rapidamente. Si può interpretare ciò immaginando che la sottile fascia d'aria surriscaldata, staccandosi dal suolo, provoca un importante richiamo d'aria circostante che si mescola (rotori) all'aria della bolla e la raffredda. Si può dunque concludere che per innescare l'ascendenza termica è necessaria una forte differenza di temperatura e che è la differenza di umidità che assicura in seguito la sua salita.
Devo riconoscere che sono troppo numerosi i manuali di meteorologia per piloti che sono non molto chiari e non molto realisti per quanto riguarda la struttura termica della bassa troposfera. Nella maggior parte dei casi nemmeno si parla di fascia convettiva, nozione essenziale per comprendere le tecniche di previsione termoconvettive e interpretare correttamente l'emagramma. La figura 3 mostra a sinistra le rappresentazioni grafiche irrealiste delle temperature dentro (curva nera) e fuori dalle ascendenze (curva chiara) fatta dalla maggior parte dei manuali. Mi pare che la rappresentazione a destra risponda più alla realtà.
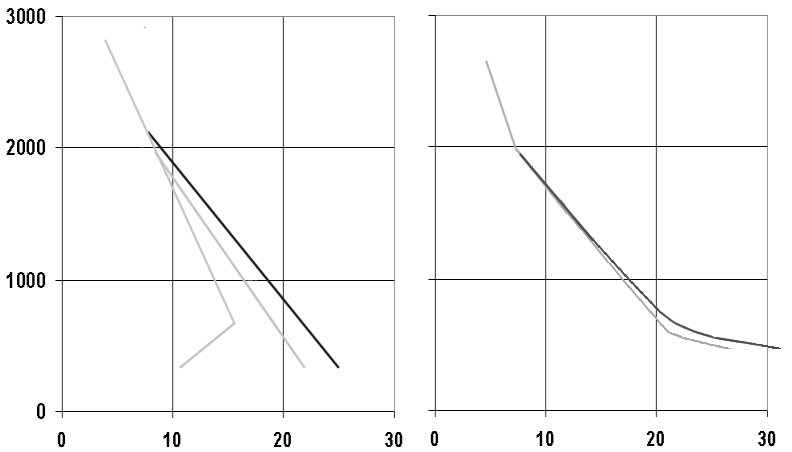
figura 3
Se prendo la figura dell'articolo precedente riguardante l'adattamento della previsione del sondaggio previsto (modello GFS), la curva di temperatura indicata dalla freccia piena rappresenta il profilo di temperatura prevista dal modello (figura 4, sinistra). Poiché il modello non "vede" le valli, la curva deve essere adattata in considerazione del maggior riscaldamento del piccolo volume d'aria all'interno della valle stessa. A causa di questo fenomeno il profilo della temperatura nelle Alpi assomiglia più a quello indicato dalla freccia vuota (figura 4, destra).
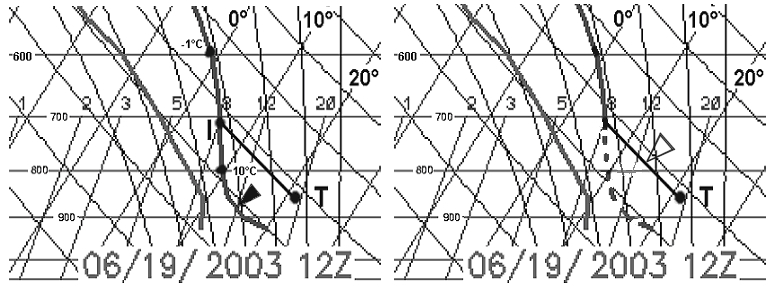
figura 4
Certi volovelisti e meteorologi francesi ad americani hanno dimostrato empiricamente una relazione tra lo spessore della fascia convettiva e la potenza delle termiche. Più la fc è spessa, più forti sono le ascendenze. Per noialtri liberisti ciò non ha, secondo me, molta importanza. Il limite per noi non è la forza delle ascendenze, spesso troppo forti e turbolente per le nostre fragili ali, semmai il plafond. Più è alto, ed io amo i plafond oltre i 4000m sfortunatamente molto rari, più la nostra libertà e la nostra tranquillità nelle scelte tattiche del percorso sono migliori. Un plafond non molto alto (per esempio 3000m per le Alpi) rende il volo di distanza nettamente più difficile.
Alla luce di tutto ciò che è stato detto finora si può capire perché una sorgente termica, per buona che sia (scura, secca, concava), non potrà generare una buona ascendenza termica se l'atmosfera non lo permette. Immaginiamo un'eccellente sorgente termica, ben soleggiata, su una piccola isola al centro di un oceano freddo. Siccome la superficie dell'oceano non si riscalda che molto lentamente e poco sotto l'azione del sole, non avremo che pochi fenomeni convettivi nella bassa troposfera a contatto con l'acqua. La fascia convettiva sovrastante sarà dunque molto sottile o addirittura inesistente. Malgrado le sue qualità termiche intrinseche, la nostra piccola isola non vedrà dunque le sue bolle termiche, prodotte dalla superficie, innalzarsi molto in alto. D'altra parte, Buz (ex-URSS, 1975) ha dimostrato che più la superficie al suolo era contrastata (superfici molto calde accanto a superfici più fresche) e migliori erano le ascendenze termiche. Io penso che non c'è bisogno di dimostrare che le nostre valli alpine offrono una superficie (suolo) molto contrastata.
Un'altra convinzione che bisognerà abbandonare è quella della stabilità atmosferica. Si sentono spesso dei piloti dire che la giornata è stabile perché non hanno incontrato delle buone ascendenze termiche. Ma da quando c'è il sole si forma obbligatoriamente una fascia convettiva nella quale regna un'instabilità termoconvettiva. Ma questa fascia è troppo sottile, le ascendenze non sono facilmente sfruttabili che dagli uccelli più performanti in termini di tasso di caduta e più abili.
Dal punto di vista meccanico e dinamico, può essere utile ricordare che un'ascendenza prende schematicamente la forma d'un anello vorticoso che si sposta globalmente verso l'alto girando su se stesso attorno ad un asse anulare. La velocità verticale più elevata si trova al centro. Ella è in questo punto, più grande della velocità di salita dell'insieme del nucleo. La figura 5 mostra una sezione schematica di un anello termico. Nel corso della sua salita il vortice aumenta e diviene più largo.
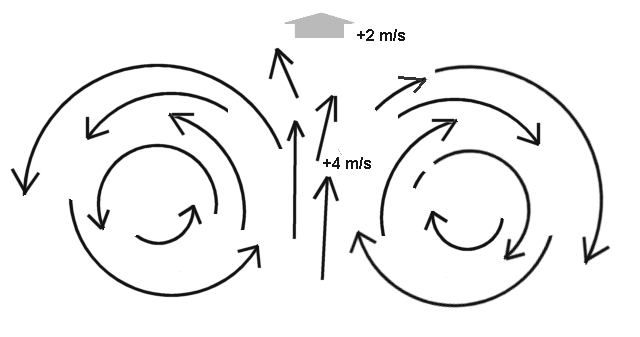
figura 5
In realtà, Lindemann ha misurato e osservato una realtà più complessa. In un'ascendenza ci sono spesso diversi noccioli più forti. Vedere la figura 6.
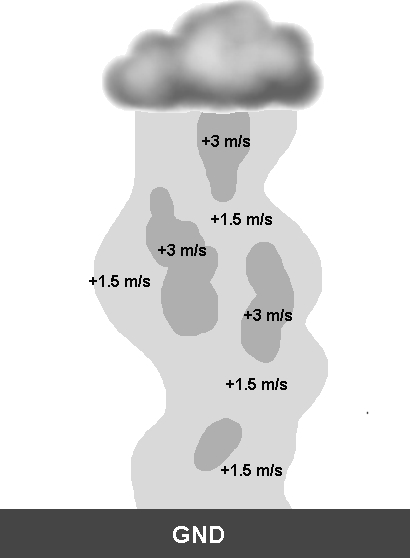
figura 6
La figura 7 mostra una carta approssimativa della ripartizione delle diverse fasce convettive situate dall'ovest valdese fino in Valais. La zona tratteggiata orizzontalmente rappresenta la fc del Plateau, limitato a sud da Blonay, Attalens, Mt-Pélerin. Può essere utile precisare che coloro che decollano dalle Pléïades o da Mauborget vanno a volare nell'atmosfera del Plateau (forse un po' influenzata anche dai laghi vicini) piuttosto che in un'atmosfera prealpina prettamente jurassiana situata più in profondità nelle piccole valli del rilievo. La zona tratteggiata in obliquo rappresenta la fc lacustre, quasi sempre poco spessa dunque poco favorevole, che si estende dal Lago Leman fino a Sion-Sierre passando attraverso il Chabais e sfumando progressivamente. E' il potente vento di valle che permette l'estensione della fresca aria lacustre così profondamente nella valle del Rodano. Ekhart (Austria, 1948) aveva già osservato e misurato, utilizzando un termogramma, l'avvezione di aria fredda al fondo di una valle simile dalla levata del vento di valle (valle di Sulzau in Austria). Più vicino a noi numerosi piloti hanno certamente notato che, durante le giornate calde, le termiche sono "paradossalmente" migliori verso e 9-10 del mattino, sui pendii a sud-est di Mayens o di Fracette (Vionnaz) che verso le 11-12 quando si instaura la brezza di valle. Più fa caldo e più l'effetto nefasto della brezza di valle (spesso d'origine lacustre) sembra manifestarsi, in profondità nella valle ed in intensità. Nelle mie statistiche personali, se si prende qualche giornata assolata e poco ventosa da aprile a agosto, si noterà in effetti che, in media, la differenza di temperatura tra Montreaux e Sion alle ore 13 è di 4-5°C in aprile e maggio, 2-3°C in giugno e 1-2°C in luglio e agosto. Ciò significa che più fa caldo e più il deficit di temperatura a Montreux si estende verso la Valais centrale. Allo stesso modo, la differenza di temperatura tra Sion e Montana durante le stesse giornate è di circa 8°C in aprile e maggio, 7°C in giugno, 6°C in luglio e 5°C in agosto. Si può quindi concludere che più fa caldo e più la fascia non adiabatica detta "stabile" (inversione, isotermia) al centro della valle principale, solitamente verso 1000-1500m di altitudine, è marcata. Ch.-P. Peguy (Francia, 1969) ha scoperto un fenomeno simile verso Nizza. Il gradiente termico sulle coste montagnose di Nizza varia in funzione della temperatura a Nizza. La relazione è quasi lineare. Se ci sono 30°C il gradiente di temperatura è uguale a 0°C, se ci sono 0°C, il gradiente sarà uguale a 1°C/100m. In altre parole più fa caldo e meno bisogna volare vicino alla larga valle se si vuol restare in aria!
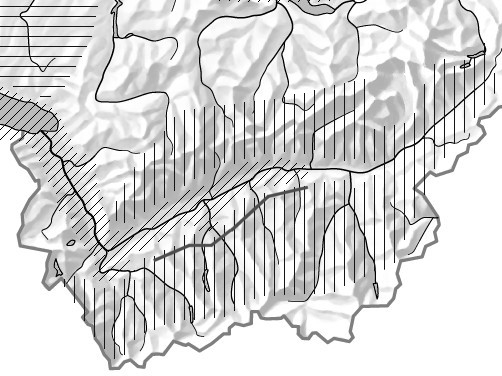
figura 7
Infine, la zona tratteggiata verticalmente mostra l'estensione della fascia convettiva alpina che è sovente sufficientemente spessa (plafond a più di 3000m) per permettere voli di distanza. Per la catena de l'Adret (catena bernese) il limite sud-est definito dal circo d'Ovronnaz e il plateau d'Aven, dal Saviése, dall'Anzére e da Montana. Per l'Ubac (Alpi vallesi) il limite nord mi sembra, secondo la mia esperienza, più in profondità nelle lunghe valli laterali. Per esempio, l'entrata della valle di Hérens (Nax, Vernamiège) può obbligarvi ad atterrare se siete troppo bassi (<2000m) durante una giornata calda. Un buon percorso di volo nelle Alpi vallesi (Ubac) al di fuori dell'influenza delle larghe valli principali, è la seguente: le Ruinettes, diga di Cleuson, Pic d'Artzinol, Sasseneire, St-Luc ma bisogna aspettare l'inizio del pomeriggio perché le facce ovest siano ben soleggiate (vedere linea spessa a zigzag, in figura 7).
Un'ultima domanda da porsi è quella della struttura termica e meccanica delle ascendenze alpine. E' la stessa di quella delle zone pianeggianti? Il manuale di previsione volo a vela dell'Organizzazione Mondiale di Meteorologia descrive le termiche alpine come più forti, più regolari (colonne piuttosto che bolle), più strette, cominciano prima e finiscono dopo rispetto alla termica di pianura. Io aggiungerei che si estendono più in alto poiché la fascia convettiva si estende spesso a più di 3000m d'altitudine e che hanno la tendenza ad essere piuttosto turbolente, soprattutto in presenza di vento. Secondo me, per noialtri parapendisti, il vento non dovrebbe essere superiore a 10 nodi (18km/h) a 700hPa, soprattutto se perpendicolare alla valle principale (nord o sud) se si vuol effettuare un volo di distanza con una certa sicurezza e serenità. Ma penso anche che le ascendenze alpine si verifichino spesso negli stessi posti, quelli particolarmente propizi al loro sviluppo. Gli abitudinari del posto le chiamano spesso "pompe del coglione".
Jochen Von Kalckreuth, nel suo celebre libro "Segeln über den Alpen" descrive la sua rappresentazione delle ascendenze alpine. Malgrado tutto il mio rispetto per questo grande pilota di volo a vela, mi è impossibile appoggiare i suoi concetti, che mi sembrano dunque tanto fantasiosi quanto attinenti a prima vista, ai risultati delle misurazioni effettuate nelle Alpi (da Neiniger per esempio). La figura 8 è tratta dal suo libro. Si constata che:
- il gradiente termico dell'atmosfera libera nella valle è di 0,75°C ogni 100m. Non c'è dunque la fascia convettiva adiabatica.
- la differenza di temperatura tra l'aria della termica e l'aria circostante è di circa 6°C all'altitudine delle creste!!! perché J. Von Kalckreuth pensa che il pendio dia assai calore alla termica durante tutto il suo percorso
- Non si fa una differenza chiara tra brezza anabatica (brezza di pendio da non confondere con adiabatico) e la termica propriamente detta.
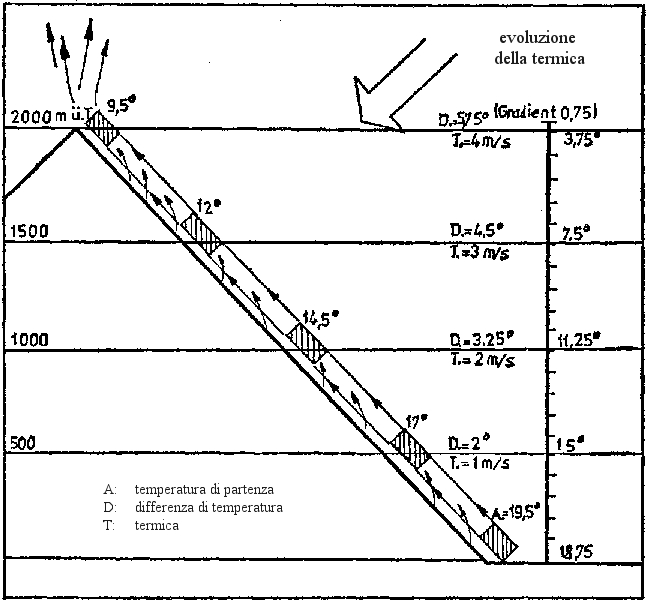
figura 8
Dalle mie ricerche bibliografiche e la mia esperienza di volo (probabilmente il pilota di parapendio è più vicino alla montagna che non un pilota di aliante) è necessario innanzitutto distinguere inizialmente il vento anabatico, molto leggero, che accarezza intimamente e pressappoco interamente tutto il pendio soleggiato e che ci permette di decollare vento in faccia, e successivamente l'ascendenza termica propriamente detta, più forte e che si stacca assai rapidamente dal pendio per alzarsi molto in alto fino alla sommità della fascia convettiva. Vedere figura 9. Per i voli di distanza, queste ultime ascendenze, che nascono sulle superfici particolarmente favorevoli al riscaldamento solare, sono più probabilmente utilizzabili che i venti anabatici. D'altra parte io credo che non ci sia alcun dubbio:
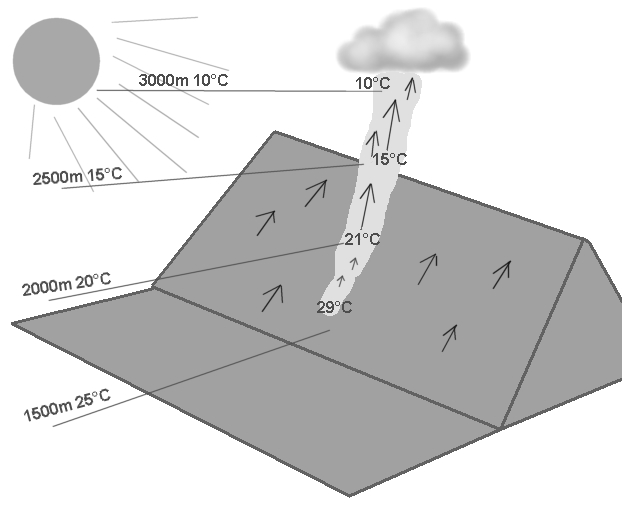
figura 9
una fascia convettiva adiabatica si sviluppa rapidamente nell'atmosfera libera della valle durante una giornata assolata. Quanto alle differenze di temperature tra l'ascendenza e l'aria circostante, mi pare molto irragionevole pensare che questa differisca molto da quella delle termiche del Plateau. L'aria della termica è certamente molto calda alla base e vicino al pendio dove il movimento d'aria è ancora molto debole ma quando le correnti d'aria ascensionali accelerano e si allontanano dal pendio, l'aria ascendente deve raffreddarsi molto velocemente per raggiungere la temperatura dell'aria circostante. Vedere la figura 9. E', di contro, possibile che le "pompe dei coglioni" abbiano per origine un insieme di superfici surriscaldate, le une sopra o accanto alle altre, che riuniscono la loro energia per rendere l'ascendenza particolarmente ben sviluppata. Tutto questo resta chiaramente da verificare. Io non conosco sfortunatamente esperienze meteorologiche che studino questo argomento. Da fare, forse, un giorno. Voilà c'est enfin terminé!
Tiberio G. 2006-12-27About this document ...
Demistifichiamo l'emagramma, il ''temp'' ed il riscaldamento dell'atmosferaThis document was generated using the LaTeX2HTML translator Version 2002-2-1 (1.71)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html emagramma.tex
The translation was initiated by Tiberio G. on 2006-12-27
HTML modificato manualmente dal traduttore, nonché autore del sito, Tiberio Galletti.
|
questo testo può essere diffuso liberamente a patto che ciò sia fatto senza fini di lucro, non sia apportata alcuna modifica a forma e contenuto e siano citati i nomi di autore (Jean Oberson) e traduttore (Tiberio Galletti) nonché le fonti dell'articolo originale (www.soaringmeteo.com) e della versione tradotta (sulparapendio.altervista.org, |
Tiberio G. 2006-12-27

